Алгоритмы раскраски графов
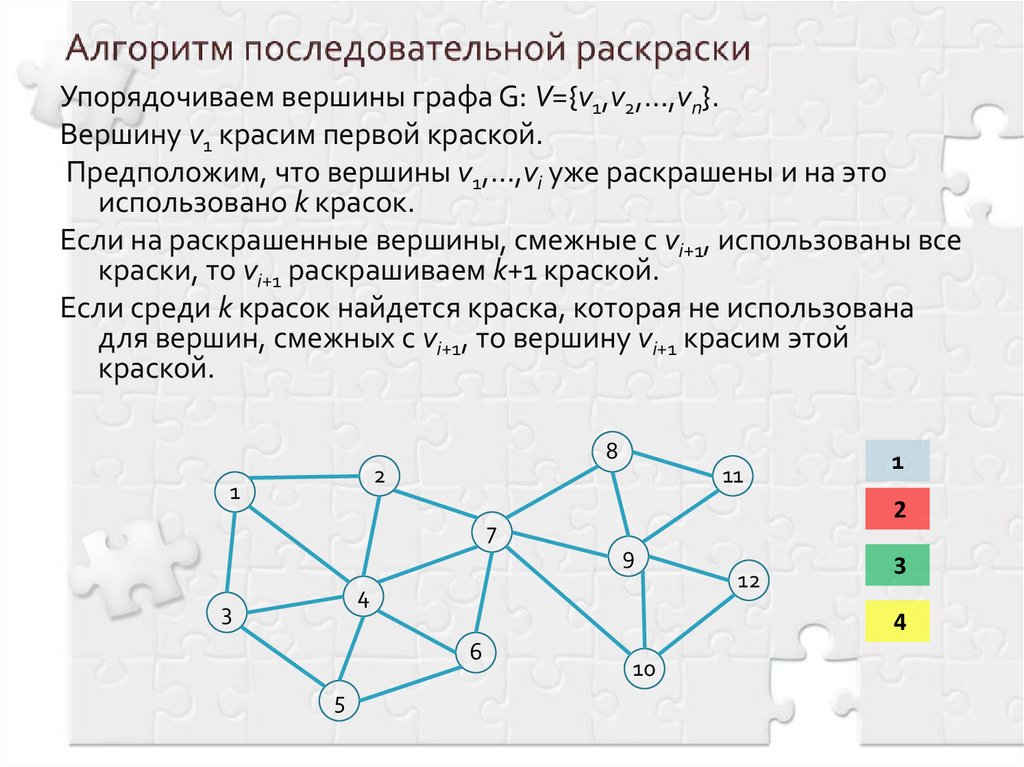
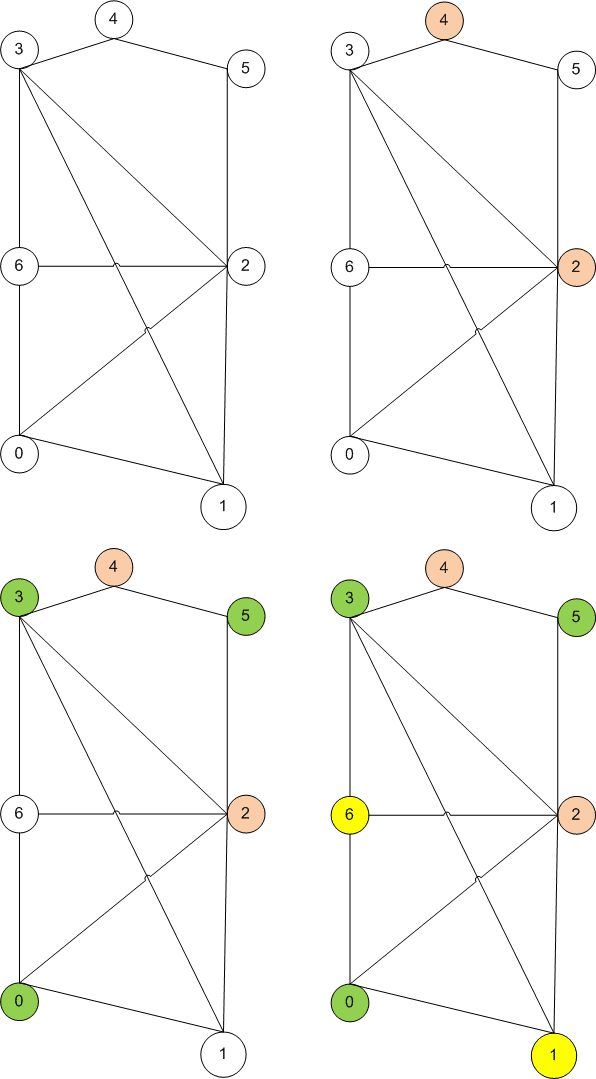
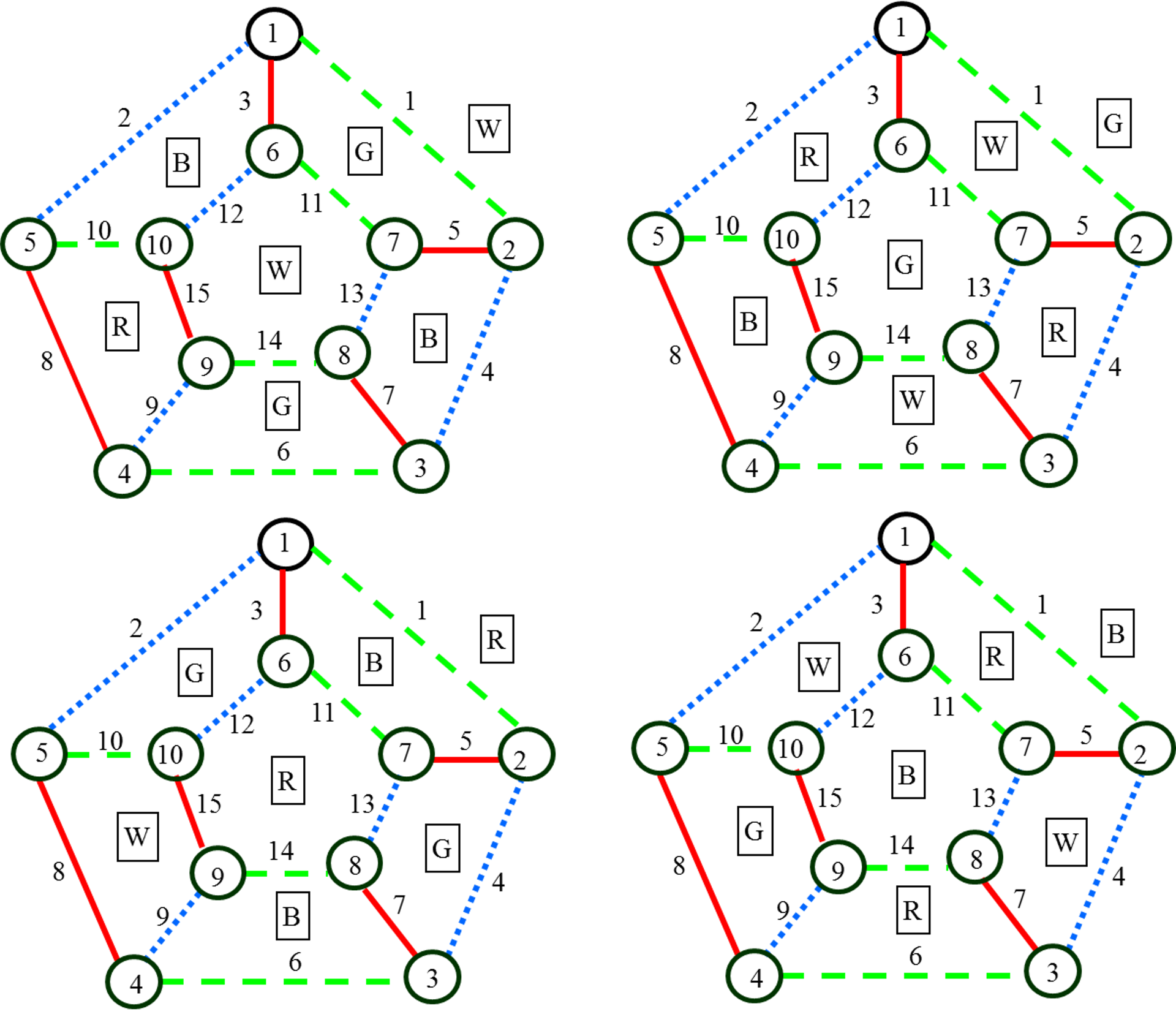
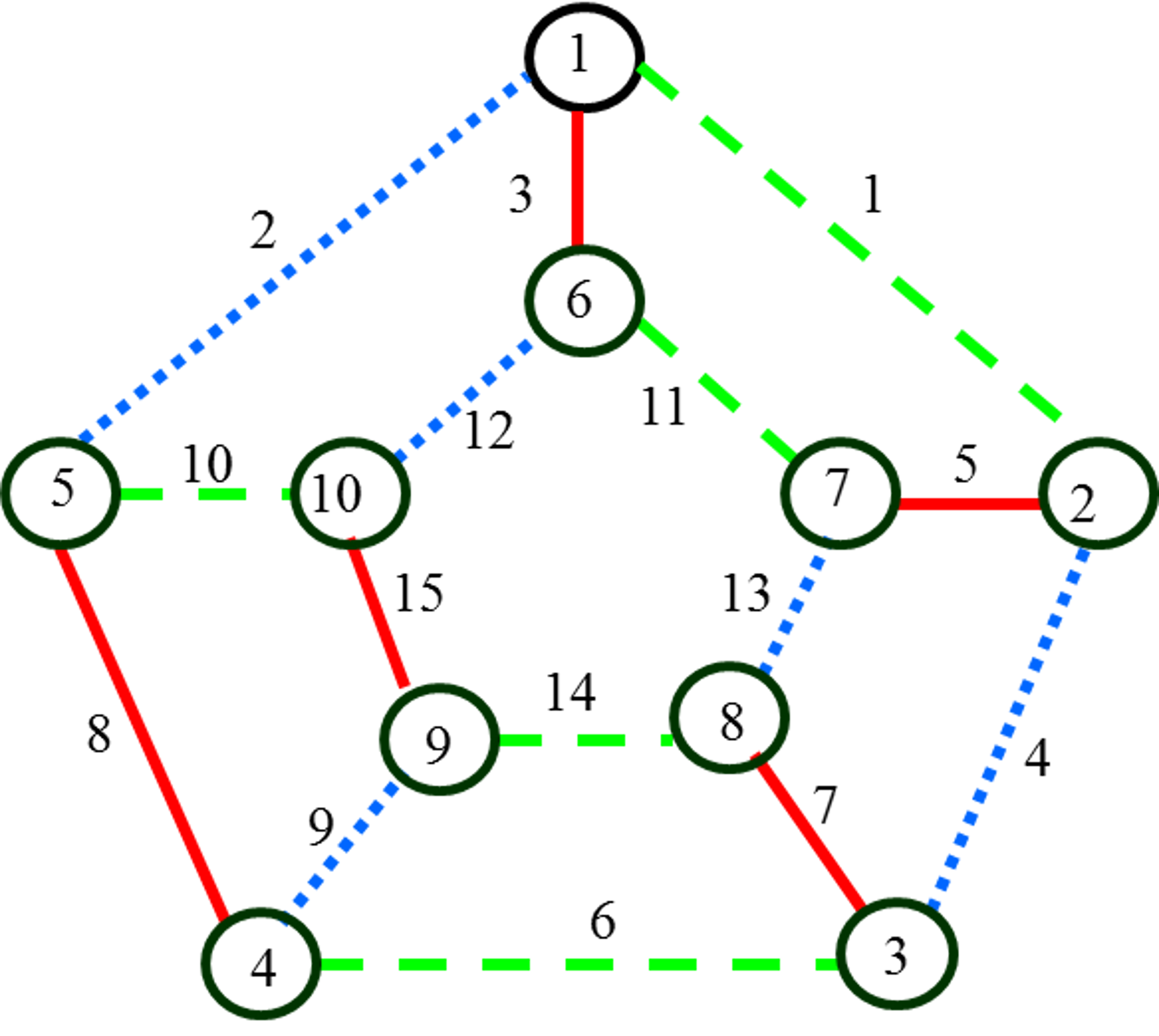
Алгоритмы раскраски графа
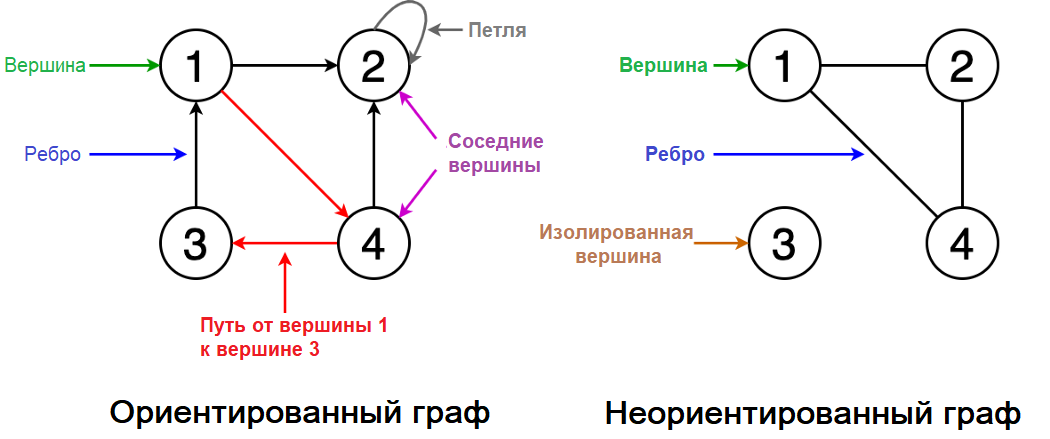
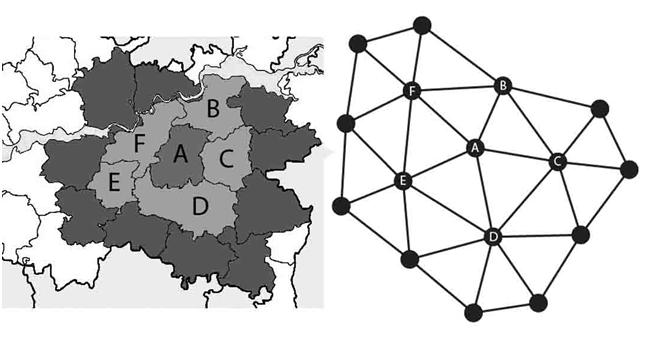
Первоначально раскраски графов были нужны для составления географических карт [1]. Сегодня же они в частности раскраска с использованием минимального количества цветов используются, например, для составления расписаний, распределения регистров в микропроцессорах, распараллеливания численных методов. Материал из Викиконспекты. Перейти к: навигация , поиск. Определение: Правильной раскраской англ. Основная статья : Хроматический многочлен.
![Вы точно человек? [В работе] Конспект лекции по раскраскам](https://cf.ppt-online.org/files/slide/7/7KoZr0ApkjGWlYf1C6mwdXPHb8t4NeuLFsEnJU/slide-7.jpg)
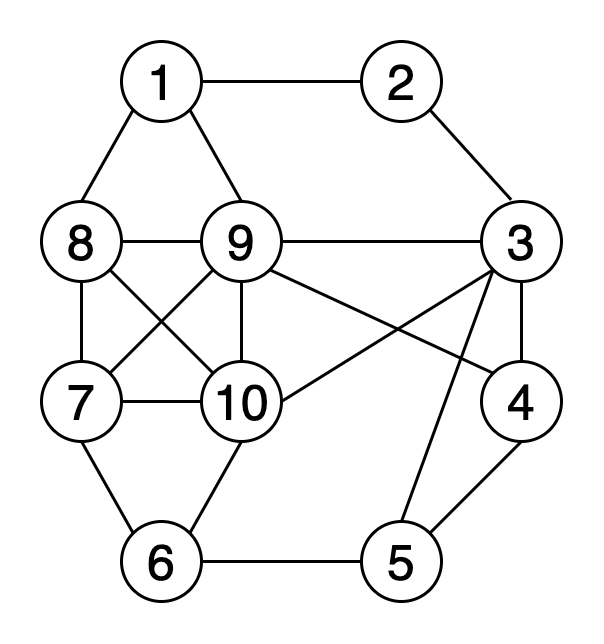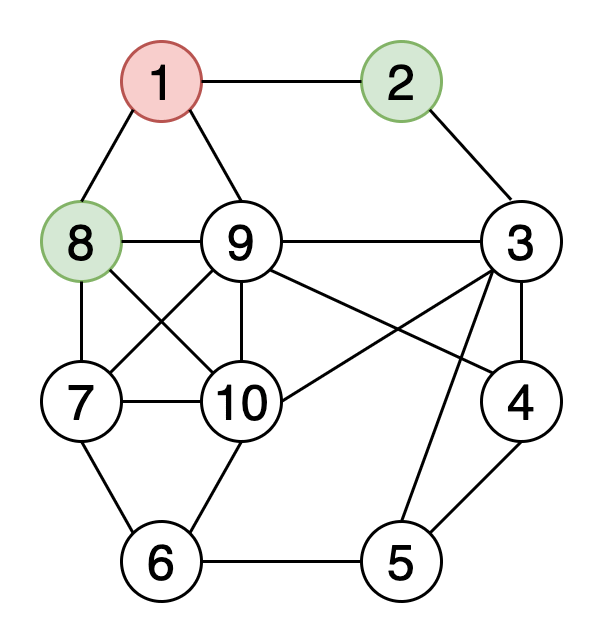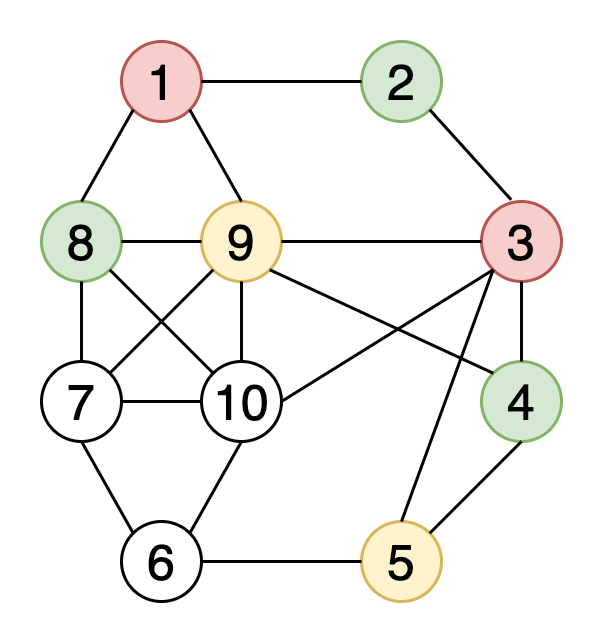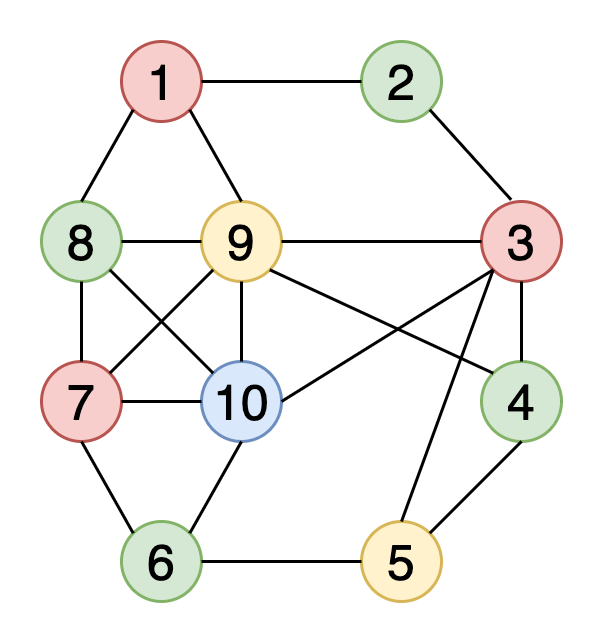


![[В работе] Конспект лекции по раскраскам [moda-foto.ru]](https://i.ytimg.com/vi/TTrNUyFR9fQ/sddefault.jpg)
Санкт-Петербургский государственный университет — старейший и один из крупнейших и ведущих классических университетов Российской Федерации, основанный в году. Сегодня он является научно-образовательным центром мирового значения и занимает высокие позиции в международных рейтингах. Здесь учатся более 20 тысяч студентов из десятков стран мира, работают лауреаты Нобелевской и Филдсовской премий, запускаются прорывные исследовательские проекты и совершаются открытия. Вы тоже можете стать частью истории.


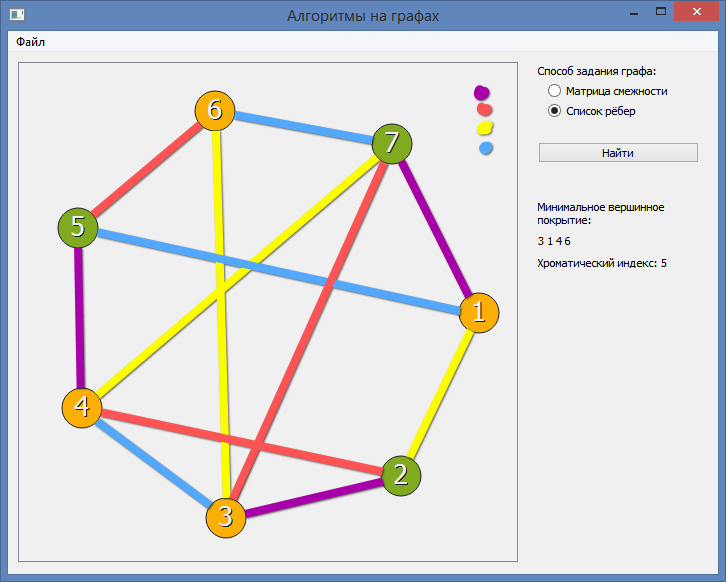
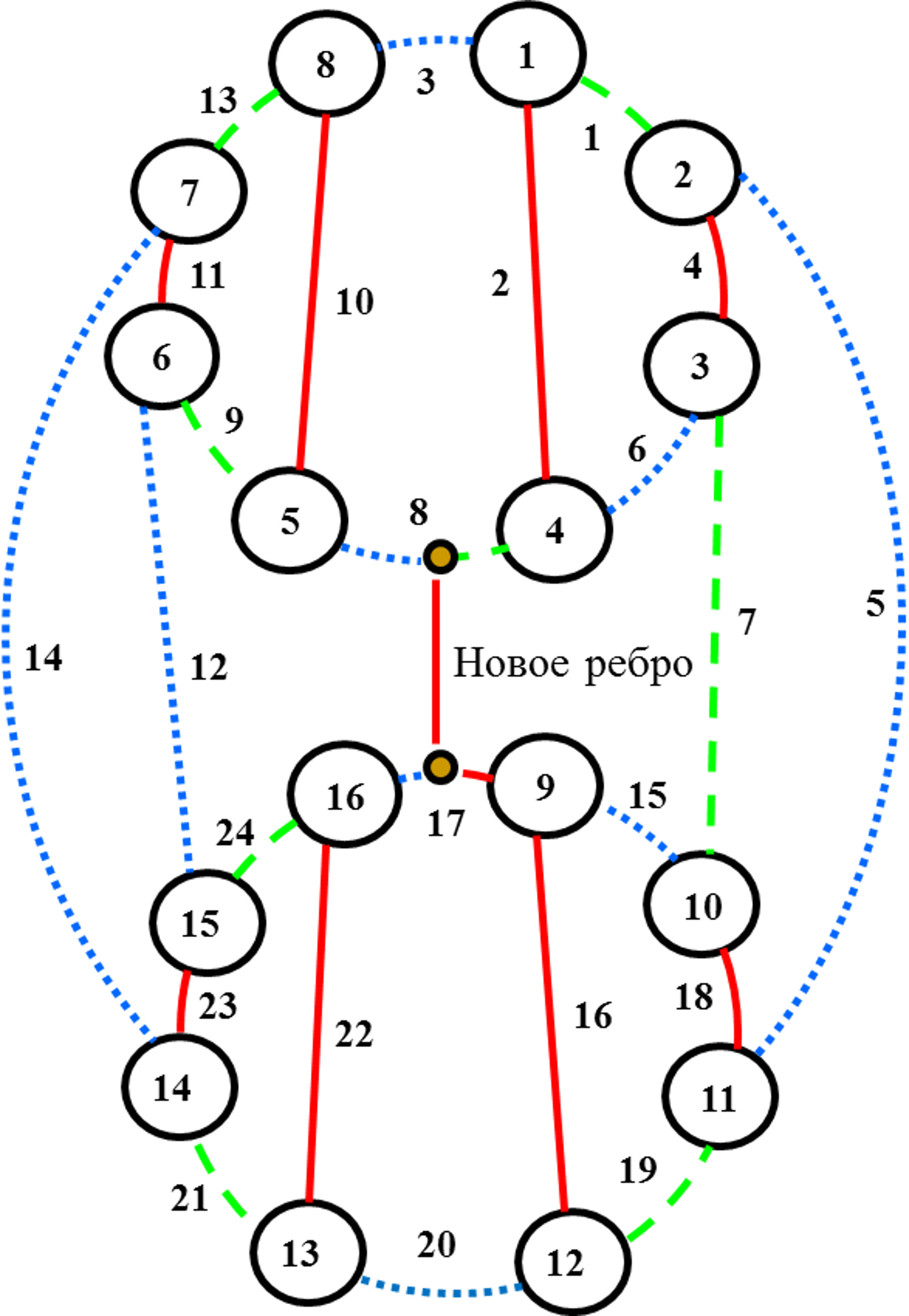


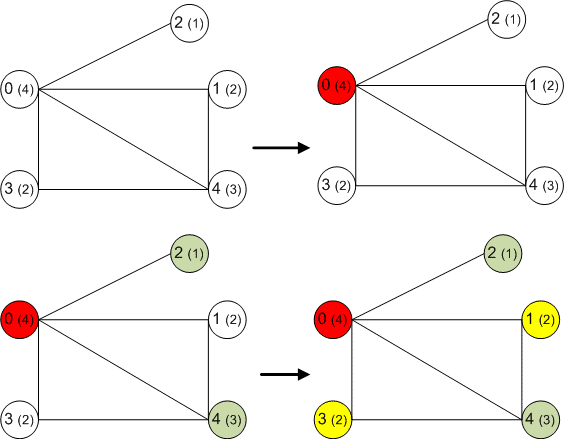
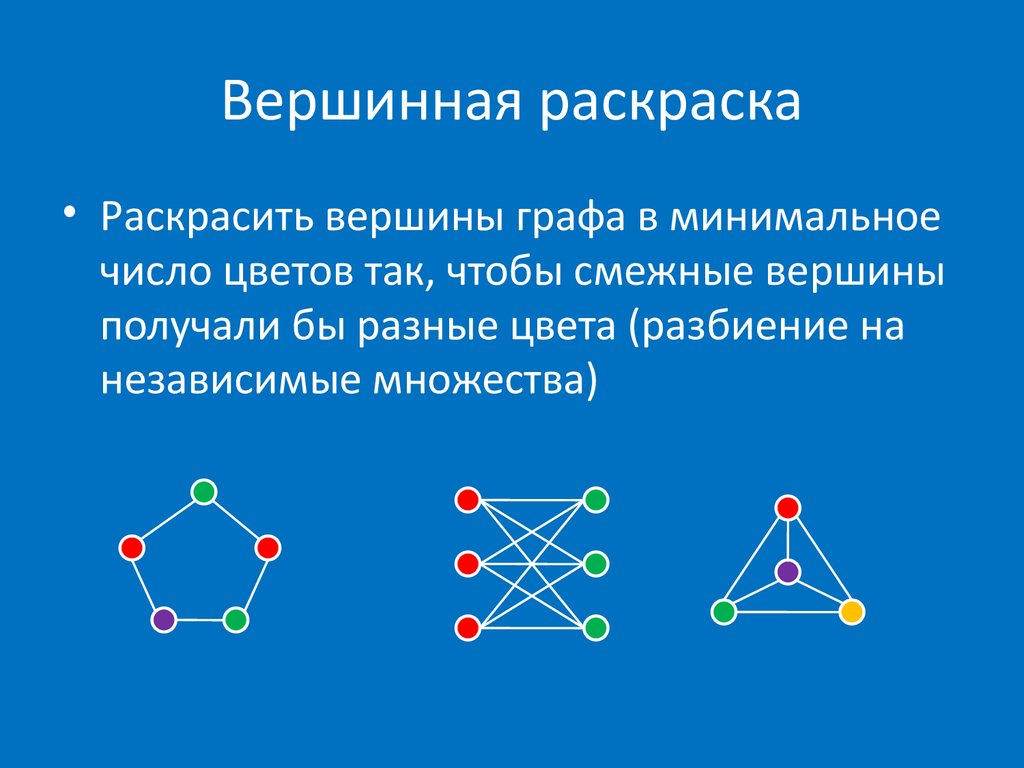
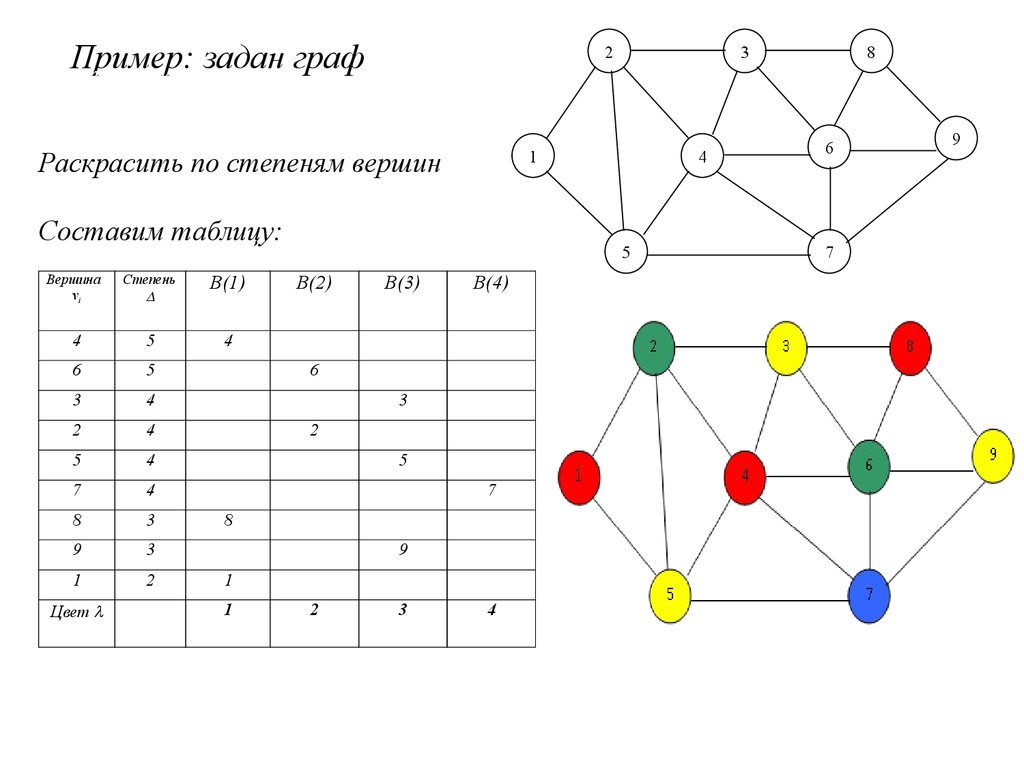
Категория: Математика. Похожие презентации:. Системы логических уравнений. Алгоритмы раскраски графа. Алгоритмы раскраски графа Необходимо раскрасить вершины графа таким образом, чтобы смежные вершины были окрашены в разные цвета.